La hausse récente de la volatilité des marchés a remis le risque au centre de nos préoccupations.
Qu’elle soit passive – par diversification de portefeuille, ou active – par des opérations de couverture, la gestion des risques est souvent liée à la notion de corrélation. Ainsi, la diversification sera d’autant mieux réussie que les actifs du portefeuille seront peu corrélés entre eux; à l’inverse, la couverture ne sera efficace que si la corrélation entre l’actif à protéger et l’instrument de couverture est élevée.
Vu l’importance du rôle joué par la corrélation dans la gestion du risque, nous vous proposons de revoir quelques propriétés, souvent méconnues, de son avatar le plus utilisé: le coefficient de corrélation, ou corrélation de Pearson1. Nous partagerons aussi, dans deux autres articles, quelques expériences passées et des techniques qui semblent revenir d’actualité.
La linéarité – rien qu’elle!
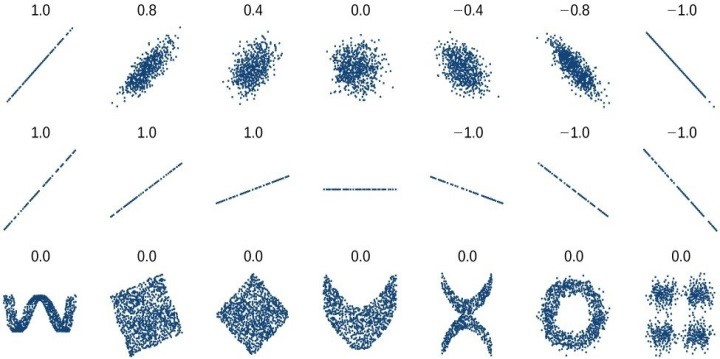Par définition le coefficient de corrélation reflète l’existence d’une relation linéaire. Il varie toujours entre -1 et +1; égal à 1, il indique la présence d’une relation linéaire positive entre les observations. Les exemples de coefficients calculés pour différents nuages de points dans les deux premières lignes du tableau ci-contre illustrent cette notion de correspondance linéaire.
En revanche si le coefficient de corrélation est proche ou égal à zéro la seule affirmation possible est: il n’y a pas de relation linéaire. Car d’autres formes de relations sont possibles même avec une corrélation nulle, comme en témoignent les exemples sur la troisième ligne. Des relations claires entre les variables peuvent donc passer inaperçues si on se contente de la seule lecture des coefficients numériques. La visualisation des nuages de points est donc chaudement recommandée pour éviter des interprétations hâtives.
Seulement les observations – rien qu’elles!
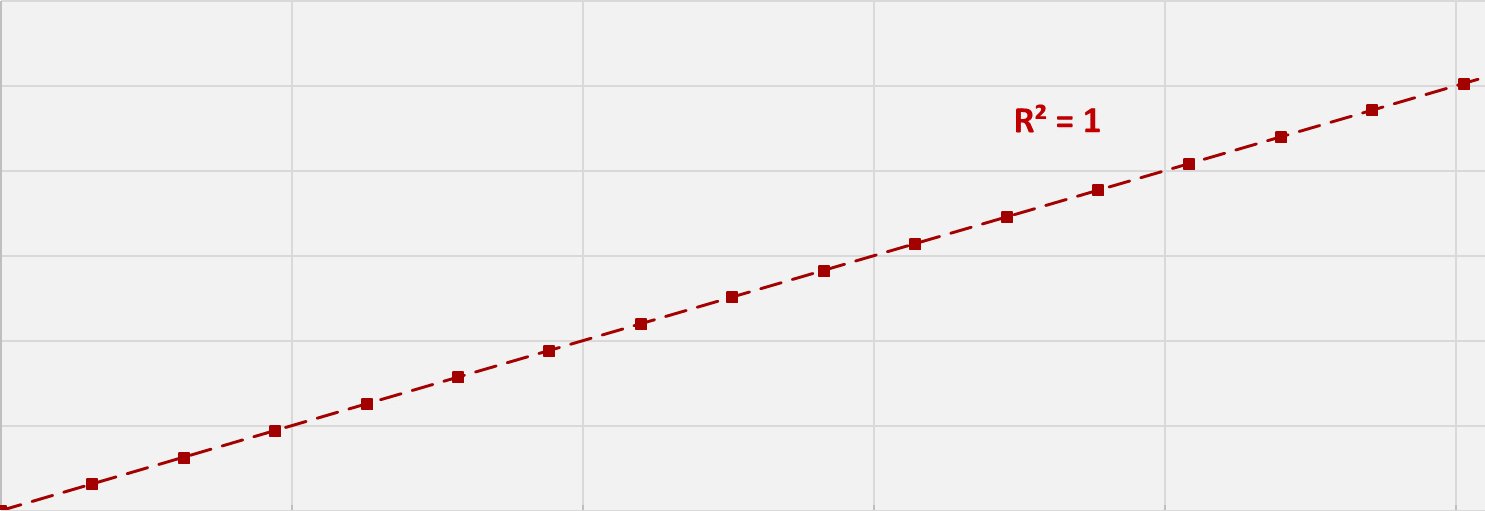Le carré du coefficient de corrélation, noté R2, est souvent utilisé pour qualifier la qualité d’une régression linéaire. R2 représente la part de la variance de la série d’observations qui est reprise ou expliquée par la régression linéaire. Plus la valeur de R2 est proche de 1, plus cette part expliquée est grande, et plus les observations sont alignées. C’est le cas de figure ci-contre où une valeur 1 de R2 indique le parfait alignement d’une série de mesures prises à des intervalles de temps réguliers.
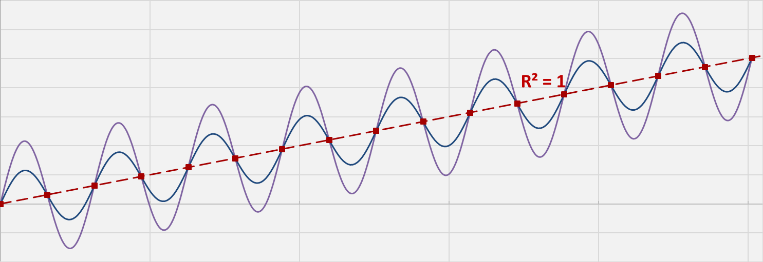Est-il juste d’en déduire que la variable observée est une fonction linéaire du temps? Pas vraiment! Car il existe une infinité de fonctions possibles qui partagent la même tendance linéaire et qui passent par les mêmes observations.
Ce qui est vrai pour l’échantillon – i.e. l’existence de la relation linéaire – peut se révéler faux pour l’ensemble de la population – dans notre exemple la relation peut tout aussi bien être une fonction sinusoïdale du temps.
Même si la corrélation observée est très forte, il faut rester prudent et éviter une généralisation pour la partie de la population non-observée, hors échantillon.
Le quartet d’Ascombe
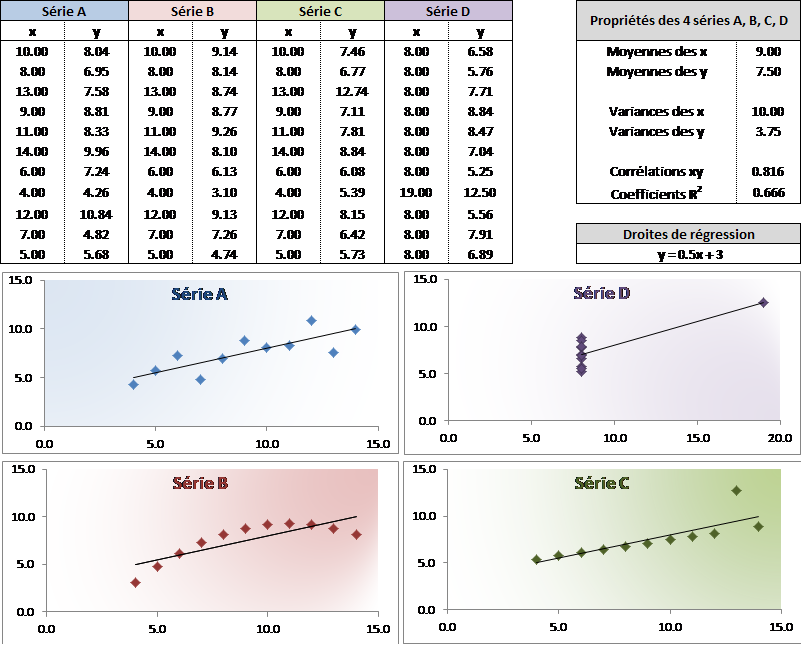
Un autre exemple qui illustre une fois encore l’utilité des représentations graphiques des données analysées a été construit et proposé en 1973 par le statisticien Francis Ascombe.
Il s’agit de quatre séries de données qui ont en commun les mêmes moyennes, les mêmes variances, les mêmes coefficients de corrélation et les mêmes droites de régression. Pourtant les séries sont très différentes les unes des autres, comme le montrent leurs graphes respectifs.
Corrélation n’est pas causalité
Si nous permutons les variables dont on calcule la corrélation, la valeur du coefficient ne varie pas. Le rôle des deux variables est parfaitement symétrique. Le coefficient de corrélation tel quel ne peut donc pas indiquer un effet de causalité.
Corrélation n’est pas relation
Entre 1999 et 2010 on a observé une corrélation de 0.957 entre le nombre de morts «tombés du lit» aux USA et le nombre d’avocats à Puerto Rico! Cet exemple absurde2 illustre que la corrélation entre deux variables peut être élevée sans qu’il existe de lien entre ces variables: par pure coïncidence.
Retenons en synthèse que le coefficient de corrélation indique la «qualité linéaire de la tendance» mesurée sur l’échantillon des observations, ni plus ni moins.
Alternative novatrice
Pour lutter contre la complexité, parfois rédhibitoire, des outils de gestion du risque ou d’allocation proposés aux investisseurs professionnels, nous proposons des solutions intuitives et rapides, simples à appréhender et faciles à calculer.
En particulier, Equilium©, un modèle novateur de simulation qui évalue l’impact sur le portefeuille de votre choix de scénarios de marché spécifiques.Il permet d’analyser, de manière intuitive et rapide, des scénarios simples ou complexes, inspirés du passé ou totalement inédits.
Equilium© accompagne l’investisseur dans l’évaluation d’un nouvel investissement, le calibrage d’une couverture de risque ou le test de robustesse de son allocation, dans la perspective de scenarios de marché de son choix ou générés par le modèle.
Notre approche et ses outils sont pensés, testés et utilisés par leurs concepteurs depuis 2009, nos solutions sont sources de surperformance.
1. Il existe d’autres mesures de corrélation telles que le quotient de corrélation, ou les corrélations de rang de Spearman ou de Kendall.
2. Vous trouverez cet exemple, et des milliers d’autres, sur «Spurious correlations» – www.tylervigen.com