Dans la pratique du calcul de corrélation nous sommes confrontés à faire des choix.

Parmi ces choix, certains sont assez simples, tels le type des données (prix ou rendements) ou leur fréquence (mensuelle, quotidienne). D’autres sont plus techniques, comme le poids des observations (surpondérer ou non les plus récentes) ou filtrer la saisonnalité (lissage exponentiel). D’autres choix encore relèvent de la nature du problème que l’on traite: le cours choisi (ouverture, clôture ou cours moyen), ou la mesure de corrélation appropriée (corrélation simple, directionnelle ou conditionnelle).

Selon nos choix le coefficient de corrélation varie de façon significative et donc les décisions qui en découlent. Pour illustrer cette problématique de calibrage du calcul de corrélation, revenons au printemps 2013, et imaginons que nous anticipions alors une hausse des taux US. Quelle valeur aurions-nous pu calculer alors pour le coefficient de corrélation entre les actions US (S&P 500) et les obligations en USD (Bloomberg Barclays Global Aggregate bond index)?

Impact de la période d’observation

S’il est naturel de penser que la corrélation calculée sur une plus longue période est plus stable, vu qu’un impact individuel – même hors norme – sera dilué dans une masse d’observations plus importante, on peut se demander comment varie le coefficient au cours de cette période «longue »?

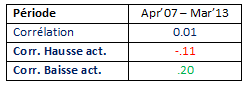
Considérons la période d’avril 2007 à mars 2013, et calculons la corrélation à partir des rendements mensuels. Le coefficient de corrélation est de 0.01 suggérant une absence de tendance linéaire entre les actions US et les obligations en USD.

Coupons cette «longue» période en deux sous-périodes égales: d’avril 2007 à mars 2010 et d’avril 2010 à mars 2013, puis calculons les coefficients de corrélation pour chaque sous-période.

Première «surprise»: la corrélation a varié de manière significative, d’abord légèrement positive (0.18), elle devient clairement négative (-0.47). Quelle est la «juste» valeur à utiliser pour la suite: la moyenne de la période longue (0.01) ou la plus récente (-0.47)?

Le film de la corrélation

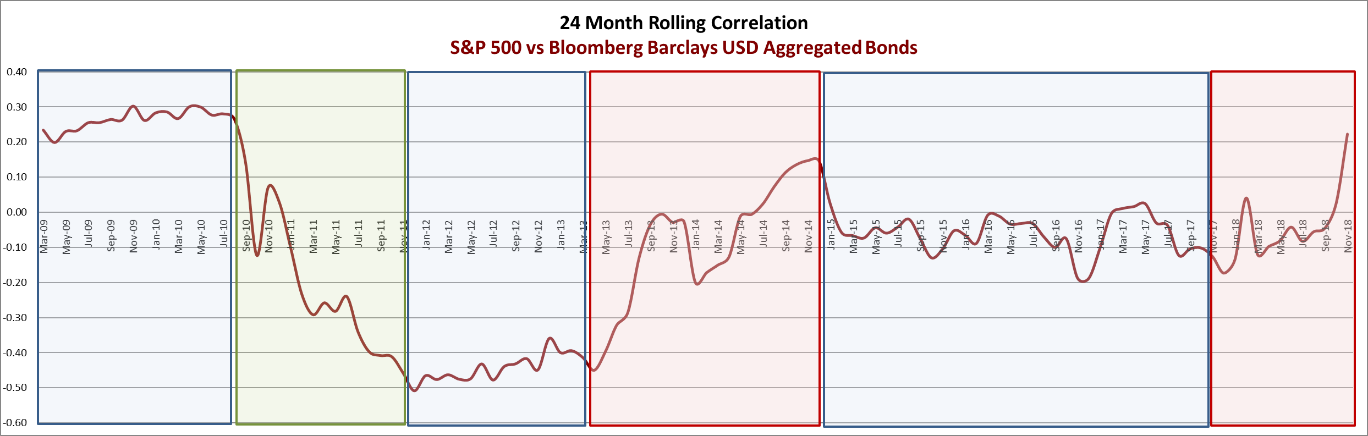
Plus que des «instantanés» de mars 2010 et 2013, nous pouvons aussi voir «le film» de la corrélation, entre les mêmes indices actions et obligations, de mars 2009 à novembre 2018. Comme le montre le graphique de la corrélation glissante sur 24 mois, nous observons 6 phases distinctes.

  1. Une période plateau de corrélation fluctuant de 0.2 – 0.3 – jusqu’en août 2010,
  2. Une phase de baisse rapide de 0.3 à -0.5 jusqu’à fin 2011,
  3. Un deuxième plateau à un niveau négatif de -0.5 à -0.4 jusqu’en avril 2013,
  4. Une phase de hausse de -0.4 à 0.15 qui se termine fin 2014,
  5. Un troisième plateau légèrement négatif, entre 0.0 et -0.2, qui se termine fin 2017,
  6. La période en cours où la corrélation est remontée de -0.2 à 0.3 fin novembre.

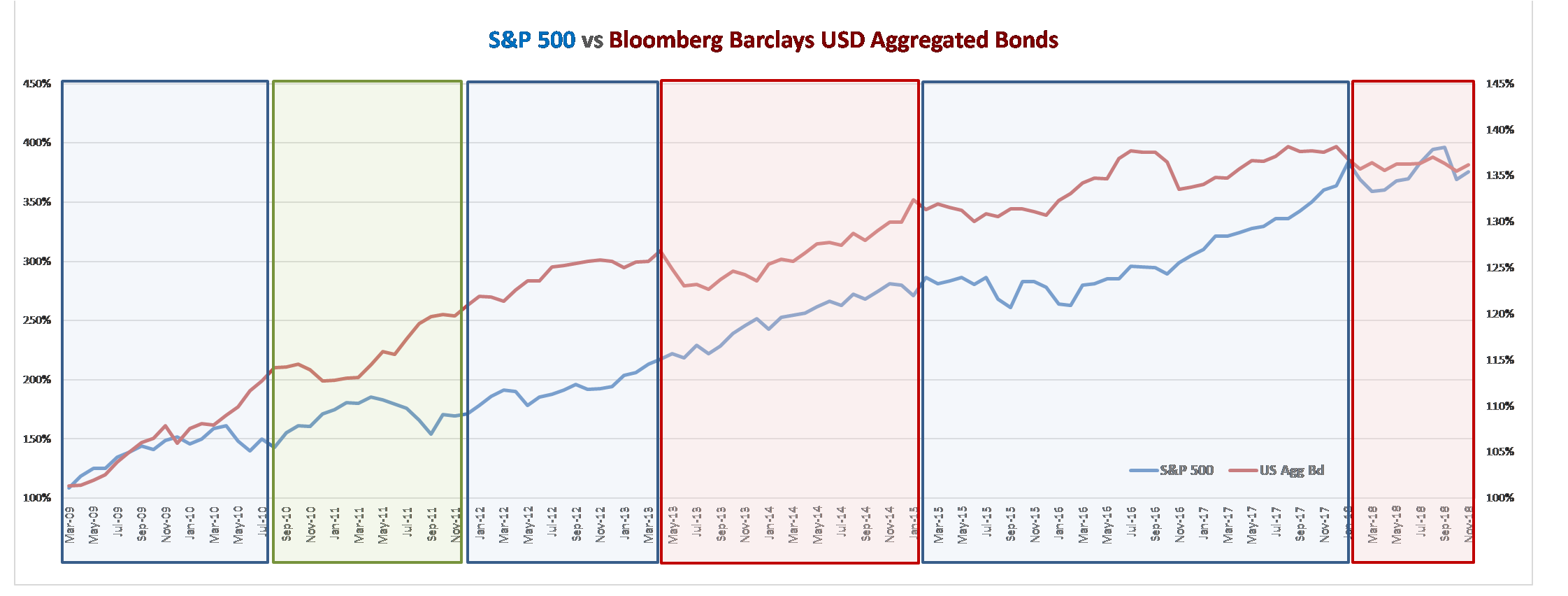
Le graphique suivant nous permet de situer ces phases dans l’évolution du prix des indices actions et obligations.

Le choix de la profondeur de calcul

Un autre paramètre d’importance lors du calcul de la corrélation est le choix de la profondeur de calcul, ainsi dans l’exemple précédent nous avons une profondeur de 24 mois. En règle générale, la profondeur doit être en rapport avec l’horizon d’investissement – un investisseur stratégique préférera une profondeur nettement plus longue qu’un intra-day trader.

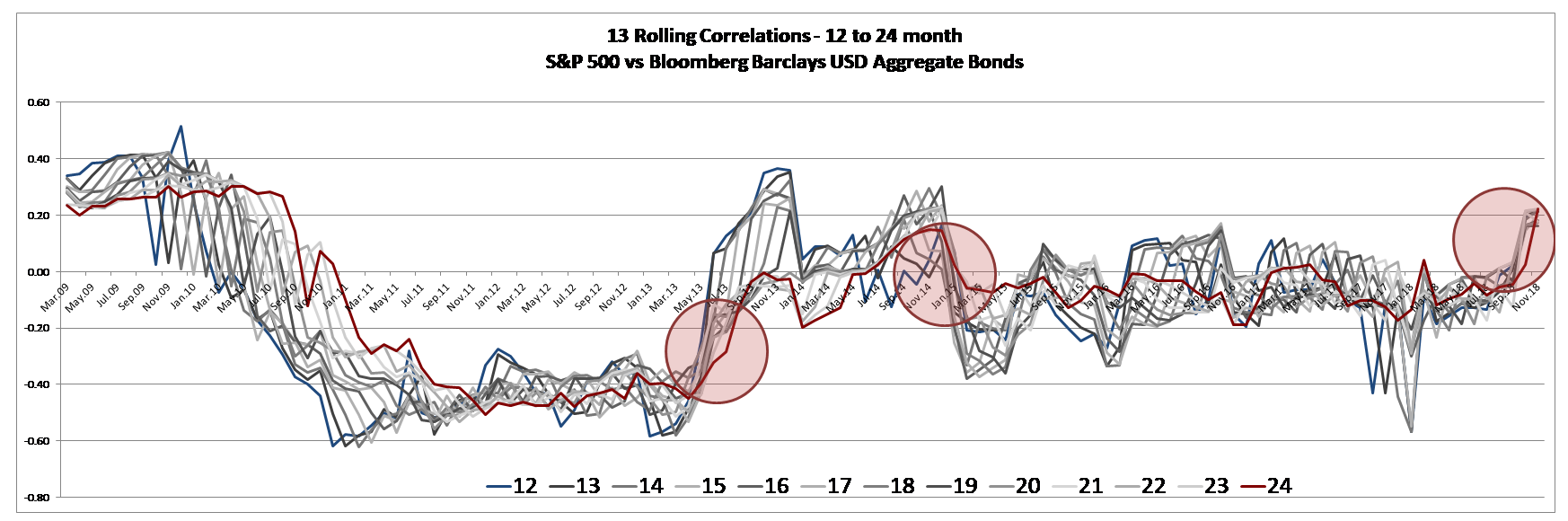
Toutefois il n’est pas rare d’hésiter entre plusieurs profondeurs possibles, toutes a priori pertinentes. Le graphique suivant présente un faisceau de 13 corrélations glissantes de 12 à 24 mois depuis avril 2007. La largeur du faisceau de corrélations à un instant donné est un message de clarté: plus le faisceau est étroit plus le coefficient de corrélation converge vers une seule valeur, levant l’hésitation du choix de la profondeur.

Ainsi dans la période actuelle la corrélation actions-obligations converge vers une valeur positive de 0.2, de mauvais augure pour une protection par diversification entre ces deux classes d’actifs.
Nous expliquons dans la prochaine section comment un simple artifice de calcul appliqué au coefficient de corrélation permet d’améliorer de façon significative la performance de l’allocation d’un portefeuille.

Asymétrie des corrélations directionnelles

Sans doute avez-vous déjà remarqué que la diversification semble être plus efficace quand le marché monte (et que l’on n’en veut pas), que lorsqu’il baisse et que soudain la diversification disparaît (avec une partie du portefeuille)? Au cœur de cette problématique on trouve l’asymétrie entre les corrélations à la hausse et les corrélations à la baisse1.

Reprenons l’exemple des actions US et des obligations globales en USD, pendant la période d’avril 2007 à mars 2013, et effectuons le calcul des corrélations en situation de hausse, respectivement de baisse, du cours des actions.

Nouvelle «surprise»: les corrélations à la baisse ont étés positives (0.2) pour la période observée, alors que les corrélations à la hausse ont été légèrement négatives (-0.1). Cas de figure particulièrement désagréable si l’on cherche à diversifier le risque d’un portefeuille en actions US par des obligations en USD.
Les exemples d’instabilité et d’asymétrie des corrélations que nous venons de voir sont particulièrement fréquents dans la pratique opérationnelle. S’il est important de les identifier il est surtout important de les traiter d’une manière appropriée.

Reprenons encore une fois notre exemple sur la même période d’observation, et calculons les corrélations directionnelles conditionnées cette fois par une hausse, puis une baisse du cours des obligations en USD.

Troisième «surprise»: les corrélations directionnelles, conditionnées cette fois par le cours des obligations, sont différentes de celles que nous avions obtenues pour le marché actions. De surcroît le phénomène de perte de diversification s’amplifie vu que la corrélation passe de 0.2 à 0.43.

Nous avons donc une corrélation conditionnelle à la hausse des taux de 0.43, qui reflète spécifiquement notre hypothèse de hausse des taux d’avril 2013.

Autres mesures de corrélation

Il existe des techniques plus avancées pour évaluer les interactions entre classes d’actifs ou facteurs de marché. On peut penser à des modèles basés sur les séries temporelles, qui visent à stabiliser la corrélation, ou les modèles de copula qui permettent de mieux traiter les distributions non-Gaussiennes, ou encore les interrelations proposées par les réseaux neuronaux. Mais ces approches sont exigeantes en expertise, gourmandes en technologie, et peuvent se révéler difficiles d’accès, voire inaccessibles, pour une application au quotidien.

 

Alternative novatrice

Pour lutter contre la complexité, parfois rédhibitoire, des outils de gestion du risque ou d’allocation proposés aux investisseurs professionnels, nous proposons des solutions intuitives et rapides, simples à appréhender et faciles à calculer.

En particulier, Equilium©, un modèle novateur de simulation qui évalue l’impact sur le portefeuille de votre choix de scénarios de marché spécifiques.Il permet d’analyser, de manière intuitive et rapide, des scénarios simples ou complexes, inspirés du passé ou totalement inédits.

Equilium© accompagne l’investisseur dans l’évaluation d’un nouvel investissement, le calibrage d’une couverture de risque ou le test de robustesse de son allocation, dans la perspective de scenarios de marché de son choix ou générés par le modèle.

Notre approche et ses outils sont pensés, testés et utilisés par leurs concepteurs depuis 2009, nos solutions sont sources de surperformance.

 

A lire : Les surprises de la corrélation (1ère partie)

 

1. Nous appelons ici corrélations directionnelles les corrélations à la hausse ou à la baisse.